指数関数のグラフ（指数関数）

こんにちは！

数学の部屋のうちやまです。

今回のテーマは「指数関数のグラフ」です！

指数関数とは
指数関数のグラフ
- 指数関数のグラフのまとめ
- 底の条件について
指数関数の性質

指数関数とは

${ y = 2^x }$ や ${ y = \left( \dfrac{1}{2} \right)^x }$ のように、 ${ y = a^x }$ の形の関数を指数関数（しすうかんすう）といいます。また、このときの ${a}$ のことを底（てい）といいます。

底には条件があり、 ${ a \gt 0 }$ と ${ a \ne 1 }$ を満たしている必要があります（これについては後ほど詳しく説明します）。

指数関数のグラフ

それでは、指数関数のグラフを考えましょう。例として、 ${ y=2^x }$ と ${ y=\left( \dfrac{1}{2} \right)^x }$ のグラフを考えてみます。

まず、 ${ y = 2^x }$ のグラフは、上図のようにそれぞれの ${x}$ の値に対する ${y}$ の値を求めてみれば、ドンドン増えていくことがわかります。さらにその増え方も、急激に大きくなっていくことがわかります。よって、指数関数 ${ y=2^x}$ のグラフは上図のようになります。グラフを描くときの注意点は次の２点です。

① ${ x=0 }$ のとき ${ y=2^0=1}$ なので、グラフは点 ${ (0,1) }$ を通ります。

② ${x}$ の値が小さくなると ${y}$ の値はドンドン小さくなりますが、0になることはありません。よって、グラフは ${x}$ 軸に触れることはありません（ ${x}$ 軸が漸近線である、という言い方をすることもあります）。

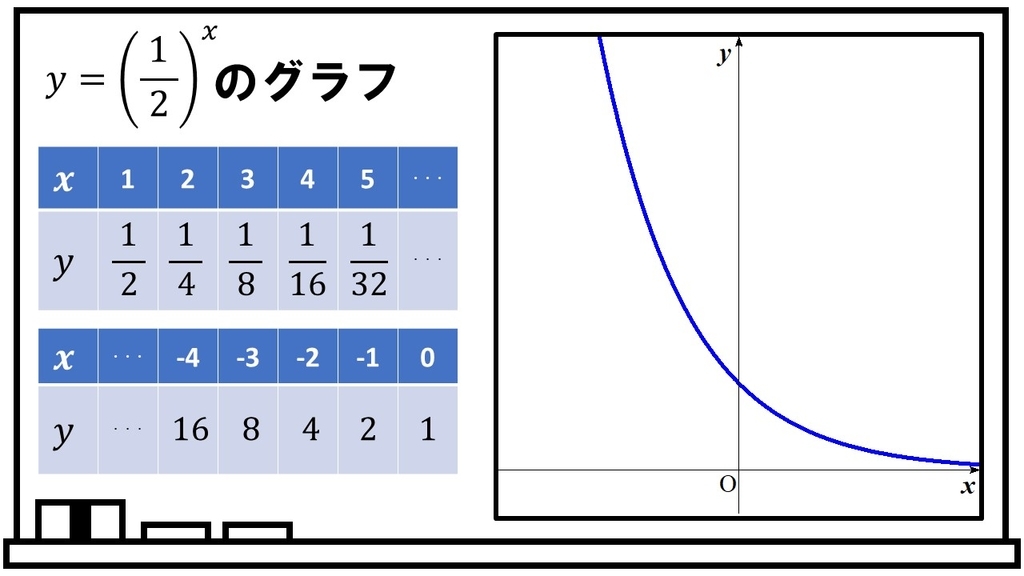
次に、 ${ y = \left( \dfrac{1}{2} \right)^x }$ のグラフも同じように考えていくと、 ${y}$ の値はドンドン(しかも急激に)減っていくことがわかります。よって、指数関数 ${ y=\left( \dfrac{1}{2} \right)^x}$ のグラフは上図のようになります。このときも、グラフを描くときの注意点は次の２点です。

① ${ x=0 }$ のとき ${ y=\left( \dfrac{1}{2} \right)^0=1}$ なので、グラフは点 ${ (0,1) }$ を通ります。 ② ${x}$ の値が大きくなると ${y}$ の値はドンドン小さくなりますが、0になることはありません。よって、グラフは ${x}$ 軸に触れることはありません（ ${x}$ 軸が漸近線である、という言い方をすることもあります）。

指数関数のグラフのまとめ

ここまでの話から、指数関数 ${ y=a^x }$ のグラフは大きく分けて2種類あることがわかります。そしてそれは底の値によって決まり、底が1より大きいとき( ${ a \gt 1 }$ のとき)は、 ${y=2^x}$ のグラフのようにドンドン増加するグラフ、底が1より小さいとき( ${ 0 \lt a \lt 1 }$ のとき)は、 ${ y=\left( \dfrac{1}{2} \right)^x }$ のグラフのようにドンドン減少するグラフになります。まとめるとまとめると下図のようになります。