2018-11-27

接線の方程式

Stage1 Stage1-15 微分法・積分法

こんにちは！
数学の部屋のうちやまです。
今回のテーマは「接線の方程式」です！

今回の問題
講義
今回の問題（再掲）
解答・解説

今回の問題

今回はこの問題に挑戦です！

f:id:s-uchiyama:20190125151331p:plain

講義

それでは、問題を解くために必要なコトを解説していきます！

準備１：直線の方程式

まず、図形と方程式で学習した「直線の方程式」を復習しておきましょう。

例えば、次の例題を考えてみましょう。

例題：点 ${ ( 1 , 3 ) }$ を通り、傾きが ${2}$ の直線の方程式を求めよ。

直線の方程式というと、よく

　　 ${ y = ax + b }$

で貫き通そうとして

解答１

傾きが ${2}$ より

${ y = 2x + b }$ とおける．

点 ${ ( 1 , 3 ) }$ を通るので

${ 3 = 2 + b }$ 　　∴ ${ b = 1 }$

よって、 ${ y = 2x + 1 \cdots}$ (答)

のような解答を書く人がいますが、時間がかかってあまりオススメできません。

「通る１点」と「傾き」が分かっている場合は、次の基本事項を使って簡単に直線の方程式を求めることが出来ます。

この基本事項を使うと

解答２

${ y - 3 = 2(x-1) }$

∴ ${ y = 2x + 1 \cdots }$ (答)

と、非常に簡単に直線の方程式を求めることが出来ますね！

これから考える「接線」も直線ですから、この基本事項がベースになります。しっかり頭に入れておきましょう。

準備２：微分係数＝接線の傾き

次に「微分係数」の復習として、２点確認しておきます。

f:id:s-uchiyama:20190125202554p:plain

１つ目は、微分係数の図形的なイメージです。「微分係数」とは「接線の傾き」のことでした。このイメージは後にも役に立つので、今のうちに覚えておきましょう。

２つ目は、微分係数の計算のしかたです。関数 ${f(x)}$ から微分係数 ${f'(a)}$ を求めるには

関数 ${f(x)}$

　↓　微分

導関数 ${f'(x)}$

　↓　 ${x=a}$ 代入

微分係数 ${f'(a)}$

という流れで求めます。

例えば「 ${ f(x) = x^2 }$ のとき ${f'(3) }$ を求めよ」といわれたら

${ f(x) = x^2 }$

　↓　微分

${ f'(x) = 2x }$

　↓　 ${ x = 3 }$ 代入

${ f'(3) = 2\times 3 = 6 }$

と求めます。

接線の方程式

それでは本題の「接線の方程式」に入ります。

まず、具体的な問題として

曲線 ${ y = x^2 }$ 上の点 ${ ( 3 , 9 ) }$ における接線の方程式を求めよ。

を考えてみましょう。

接線は直線です。【準備１】で学習したように、「通る１点」と「傾き」がわかれば、直線の方程式を求めることが出来ます。

・「通る１点」は、もちろん ${ ( 3 ，9 } )$ ですね。ちなみに、この点のことを接点といいます。

・「傾き」は、【準備２】より「接線の傾き＝微分係数」です。接点の ${x}$ 座標は ${3}$ なので、傾きは ${ f'(3) }$ を求めればよく

${ f(x) = x^2 }$ とおくと

${ f'(x) = 2x }$ より ${ f'(3) = 6 }$

よって接線は、点 ${ ( 3 ，9 ) }$ を通り、傾きが ${6}$ である直線なので

${ y - 9 = 6(x-3) }$

∴ ${ y = 6x - 9 }$

となります。ここまでは理解できましたか？

次に、これを一般化して

曲線 ${ y = f(x) }$ 上の点 ${ ( a , f(a) ) }$ における接線の方程式を求めよ。

を考えます。

先ほどと同じように考えると

・「通る１点」は ${ ( a ，f(a) } )$

・「傾き」は、接点の ${x}$ 座標が ${a}$ であることから ${ f'(a) }$

となります。

よって接線の方程式は、点 ${ (a，f(a) ) }$ を通り、傾きが ${ f'(a) }$ である直線の方程式なので

　　 ${ y - f(a) = f'(a) (x-a) }$

となります。まとめると次のようになります。

f:id:s-uchiyama:20190125170621p:plain

今回の問題（再掲）

では改めて、今回の問題を掲載しておきます。
自分の力で解いてから、下の解答・解説を読んでみましょう！

f:id:s-uchiyama:20190125151331p:plain

解答・解説

${ f(x) = x^2 - 3x + 1 }$ とおくと（※１）

${ f'(x) = 2x - 3 }$ より ${ f'(3) = 3 }$ （※２）

よって、接線の方程式は

${ y - 1 = 3(x-3) }$

∴ ${ y = 3x -8 \cdots }$ (答)

（※１）解答のように、与えられた関数の式を ${ f(x) }$ とおくと、何かと便利です。

（※２）接点の ${x}$ 座標は ${3}$ なので、 ${ f'(3) }$ が接線の傾きです。

2018-11-26

関数の増減

Stage1 Stage1-15 微分法・積分法

こんにちは！
数学の部屋のうちやまです。
今回のテーマは「関数の増減」です！

今回の問題
講義
今回の問題（再掲）
解答・解説

今回の問題

今回はこの問題に挑戦です！

f:id:s-uchiyama:20190128000006p:plain

講義

それでは、問題を解くために必要なコトを解説していきます！

関数の増減

今回の目標は、例えば

　　 ${ y = x^3 - 6x^2 + 9x + 1 }$

のような、今まで見たことのない関数のグラフを描くことです。

もちろん

　 ${ x = 1 }$ のとき ${ y = 5 }$

　 ${ x = 2 }$ のとき ${ y = 3 }$

　　　・・・

と調べて点をとり、それらを線でつなげればグラフは描けますが、少し大変です。今回はもっと簡単に、グラフの「大ざっぱな形」を描く方法を考えてみましょう。

グラフの「大ざっぱな形」とは、「グラフがいつ上がっていつ下がるのか」ということ。言い換えると「関数の値がいつ増加していつ減少するのか」ということです。では、それらを微分法の知識を使って考えてみましょう。

導関数の講義で学習したように、導関数 ${ f'(x)}$ の図形的イメージは「接線の傾き」でした。そこで、接線の傾きに注目してみます。例えば、放物線で考えてみましょう。

f:id:s-uchiyama:20190128000036p:plain

まず、関数 ${f(x)}$ の値が増加している部分の接線の傾きに注目すると、傾きは正であることがわかります。つまり、 ${ f'(x) \gt 0}$ ということです。従って

関数 ${ f(x) }$ の値が増加している（グラフが上がっている）とき、 ${ f'(x) \gt 0 }$ となる

といえそうです。

次に、関数 ${f(x)}$ の値が減少している部分の接線の傾きは負、つまり ${ f'(x) \lt 0 }$ ということですので

関数 ${f(x)}$ の値は減少している（グラフは下がっている）とき、 ${ f'(x) \lt 0 }$ となる

といえそうです。

さらに、関数 ${f(x)}$ の値が一定になる部分（減少から増加に変わる部分）の接線の傾きは０、つまり ${f'(x)=0 }$ ということですので

関数 ${ f(x) }$ の値が一定になるとき、 ${ f'(x) = 0 }$ となる

といえそうです。

このように、 ${f'(x)}$ の符号を調べれば関数 ${ f(x)}$ の値の増加・減少の様子がわかる、ということです。

グラフの描き方

では、今の話をベースにして、先ほどの関数 ${ y = x^3 - 6x^2 + 9x + 1 }$ のグラフを描いてみましょう。

グラフは次の３つのStepで描くことができます。

１つずつ、詳しくみていきましょう。

Step1： ${f'(x)=0}$ となる ${x}$ を求める

${f'(x)}$ の符号で増加・減少の様子がわかるのですから、まず ${f'(x)}$ を求めるのは自然なことですね。

今回は ${ f(x) = x^3 -6x^2 + 9x + 1 }$ とおくと

${ f'(x) = 3x^2 - 12x + 9 }$

${ = 3(x^2-4x+3 ) }$

${ = 3(x-1)(x-3) }$

となります（因数分解した理由はこの後すぐにわかります）。

そして、増加と減少が切り替わる部分を求めるために ${ f'(x) = 0 }$ を解きます。

今回は ${f'(x) = 0 }$ すなわち ${ 3(x-1)(x-3) = 0 }$ より ${ x = 1 , 3 }$ です。あらかじめ因数分解しておいたので、ラクに解くことができました。

Step2：増減表をかく

次に、関数の値の増加・減少の様子を、「増減表」と呼ばれる表にまとめます。

増減表は３行の表で、１行目から順に「 ${x}$ 」「 ${f'(x)}$ 」「 ${f(x)}$ 」とかきます。

f:id:s-uchiyama:20190128000100p:plain

それでは１行目から順に説明していきます！

■１行目： ${ f'(x) = 0 }$ となる ${x}$ をかく

f:id:s-uchiyama:20190128000121p:plain

１行目は、Step1で求めた ${x}$ 、つまり ${f'(x) = 0 }$ となる ${x}$ をかきます。今回は ${ x = 1 , 3 }$ でしたので、小さい順に ${1}$ と ${3}$ をかきます。

■２行目： ${f'(x)}$ の符号をかく

f:id:s-uchiyama:20190128000141p:plain

２行目は、 ${ f'(x) }$ の符号を「０」「＋」「ー」でかきます。

今回はまず、 ${ x = 1 , 3 }$ のときは ${ f'(x) = 0 }$ でしたので、２行目の ${ x = 1 }$ と ${ x = 3 }$ に対応するところには「0」とかきます。

次に「・・・」で書かれている部分ですが、具体的な値を代入して考えるとわかりやすいです。

例えば ${x=1}$ より小さい部分は、 ${ x = 0 }$ を ${ f'(x) }$ に代入すると ${ f'(0) = 9 \gt 0 }$ となるので「＋」をかきます。同じように、 ${x=1}$ と ${ x=3}$ の間の部分は ${x=2}$ を代入して ${ f'(2) = -2 \lt 0 }$ なので「ー」、 ${ x = 3}$ より大きい部分は ${ x = 4 }$ を代入して ${ f'(4) = 9 \gt 0 }$ なので「＋」をかきます。

■３行目： ${f(x)}$ の増減をかく

f:id:s-uchiyama:20190128000205p:plain

３行目は、 ${ f(x)}$ の値の増加・減少の様子を「矢印」でかきます。

２行目が「＋」のときは３行目に「右上がりの矢印」を

２行目が「－」のときは３行目に「右下がりの矢印」をそれぞれかきます。

[ tex:{x=1}] と ${ x=3 }$ のときは具体的に値が求められるので、 ${ ( f(1) =) 5 }$ と ${ ( f(3) =) 1 }$ をかいておきます。

これで増減表が完成しました！

Step3：グラフをかく

Step2でかいた増減表をもとに、グラフを描きます。増減表をみれば

　 ${ x \lt 1 }$ のときは増加

　 ${ x = 1 }$ のときは一定

　 ${ 1 \lt x \lt 3 }$ のときは減少

　 ${ x = 3 }$ のときは一定

　 ${ 3 \lt x }$ のときは増加

となっていることがわかります。よってグラフは次のようになります（ ${y}$ 軸を通るので ${ y }$ 切片を求めておきます。もちろん ${f(0)}$ を計算して ${ f(0) = 1 }$ ですね）。

f:id:s-uchiyama:20190128000517p:plain

以上でグラフが描けました。講義を読んだだけではなかなか身に付かないと思いますので、具体的な問題をたくさん解いて定着させましょう。

極値

最後に新しい言葉を紹介します。先ほどのグラフを見てください。

f:id:s-uchiyama:20190128001234p:plain

このグラフにおいて

　増加から減少に変わる部分（「山」の部分）を「極大」といい、そのときの ${ y }$ の値を「極大値」

　減少から増加に変わる部分（「谷」の部分）を「極小」といい、そのときの ${ y }$ の値を「極小値」

といいます。さらに「極大値」と「極小値」を合わせて「極値」といいます。

今回の問題（再掲）

では改めて、今回の問題を掲載しておきます。
自分の力で解いてから、下の解答・解説を読んでみましょう！

f:id:s-uchiyama:20190128000006p:plain

解答・解説

${ f(x) = -2x^3 - 3x^2 +12x }$ とおくと

${ f'(x) }$

${ = -6x^2 -6x + 12 }$

${ = -6(x+2)(x-1) }$

より

${ f'(x) = 0 \Longleftrightarrow x = -2 , 1 }$

増減表は次のようになる

よってグラフは下図

f:id:s-uchiyama:20190128002810p:plain

2018-11-09

指数関数の最大・最小（指数関数）

Stage2 Stage2-14 指数関数・対数関数

こんにちは！

数学の部屋のうちやまです。

今回のテーマは「指数関数の最大・最小」です！

「指数関数の最大・最小」の解法のPOINT
例題
- 問題
- 解答
- 解説

「指数関数の最大・最小」の解法のPOINT

例えば、 ${ y = (2^x)^2 - 4 \cdot 2^x + 1 }$ という関数を考えてみましょう。

一見すると複雑な形をしていますが、よくみると「 ${2^x}$ 」のカタマリに気づくはずです。そして、例えば ${2^x = t}$ とおくと、この関数は ${ y=t^2-4t+1}$ となり、 ${t}$ の2次関数になります。2次関数であれば、平方完成して、グラフを描いて、 ${\cdots}$ のように処理することができるようになります。

このように、一見すると複雑に見えるものも、おきかえを利用することで簡単な形に直すことができる、ということが1つ目のPOINTです。

ただし、おきかえをしたときに注意しなければならないことがあります。

f:id:s-uchiyama:20181109150421j:plain

いま、 ${ 2^x = t }$ とおきかえをしました。ここで、 ${ t = 2^x }$ のグラフ（上図）を見ると、グラフは常に ${x}$ 軸よりも上側にあります。ということは、 ${t}$ は必ず ${ t \gt 0 }$ になることがわかります。つまり、この関数 ${ y = t^2-4t+1 }$ は、 ${ t \gt 0 }$ の範囲で考えなければならない、ということになります。

このように、おきかえをしたときには、新しい文字（この場合は ${t}$ ）がどのような範囲の値を取るのかを確認する必要があります（これを「変域チェック」と呼ぶことにしましょう）。これが2つ目のPOINTです。

まとめると、次のようになります。

f:id:s-uchiyama:20181109145745j:plain

例題

それでは、例題を解いてみましょう（自分で解けそうな人はやってみましょう）。

問題

f:id:s-uchiyama:20181109145800j:plain

解答

${ y = 4^x - 2^{x+1 } = (2^x)^2 - 2 \cdot 2^x }$

ここで ${ 2^x = t }$ とおくと、 ${ t \gt 0 }$

このとき

${ y = t^2 - 2t = ( t -1 )^2 - 1 }$

f:id:s-uchiyama:20181109151747j:plain

ここで

${ t = 1 \Longleftrightarrow 2^x = 1 }$

∴ ${ x = 0 }$

よって

最小値 ${-1}$ ( ${x=0}$ のとき) ${\cdots}$ (答)

解説

${ 4^x = (2^2)^x = 2^{2x} = (2^x)^2 }$ と変形できます。この変形はよく出てくるのでサッと変形できるように練習しておきましょう。

また、最小となるのは確かに ${ t=1 }$ のときですが、答えは「 ${x=\cdots}$ のとき」と書かなければなりません。ですから、 ${ 2^x = t }$ の関係から ${x}$ の値を求めます。 ${t}$ のまま答えとしないよう気をつけましょう。

今回はここまでです。

最後までお読みいただきありがとうございました！

2018-10-31

指数の復習

Stage1 Stage1-14 指数関数・対数関数

こんにちは！
数学の部屋のうちやまです。
今回のテーマは「指数の復習」です！

指数とは？

これから「指数関数」という単元を学習していきます。

「指数」は中学数学で学習済みですが

「あれ？指数って何だったっけ？」

という人のために、指数の復習から始めましょう。

例えば ${2^5}$ という数について

「何と読むか」

「どういう意味か」

が言えますか？

正解は

「2の5乗と読み」

「2を5回かけるという意味」

です。

つまり

${ 2^5 = 2 \times 2 \times 2 \times 2 \times 2 = 32 }$

ですね。

このとき、 ${ 2^5 }$ の「小さい5」の部分を「指数」といいます。

ここまでは理解できましたか？続いて「指数法則」を復習しましょう。

指数法則

指数の計算は、次の「指数法則」を使うと簡単に行うことができます。

f:id:s-uchiyama:20181122235343j:plain

例えば

　 ${ a^5 \times a^3 = a^8 }$

　 ${ (a^3)^4 = a^{12} }$

　 ${ (ab)^4 = a^4 b^4 }$

のように使います。

今回はここまでです。
最後までお読みいただきありがとうございました！

★このページが気に入ったら、画面下の「読者になる」をポチッ！
★感想・質問は画面下の「コメントを書く」からどうぞ！

2018-10-31

指数の拡張１

Stage1 Stage1-14 指数関数・対数関数

こんにちは！
今回は、中学数学では扱うことのなかった ${2^0}$ や ${2^{-1}}$ を考えてみます。
指数の意味を考えれば、 ${2^{-1}}$ は「 ${2}$ を ${-1}$ 回かける」という意味になりそうですが…さて、どういうことなのでしょうか？？
さっそく始めましょう！

今回の目標

${2^0}$ や ${2^{-1}}$ などの値を求められる

今回の問題
講義
- 指数の拡張とは
- 指数の拡張
今回の問題（再掲）
- 解答
- 解説

今回の問題

今回はこの問題を解いてみましょう。
★解けそうな人はチャレンジしてみましょう！
★初めて学ぶ人、知識があやふやな人は下の「講義」を読んでからチャレンジしてみましょう！

f:id:s-uchiyama:20181101233812j:plain

講義

それでは、問題を解くための知識を解説していきます！

指数の拡張とは

今までは、指数は ${1,2,3,\cdots}$ という「自然数」しか考えてきませんでしたが、今回は「 ${2^0}$ 」や「 ${2^{-1}}$ 」などのように、指数を「整数」まで拡張します。

ところが、「2を0回かける」や「2を ${-1}$ 回かける」という意味で考えてもよくわかりません。そこで、「何回かける」という意味はいったん忘れて、数学的に矛盾がないように、「 ${2^0}$ 」や「 ${2^{-1}}$ 」の値を決めてみましょう。

指数の拡張

上の図を見てください。

まず、 ${ 2^1=2　,　2^2=4　,　2^3=8 }$ となるのは良いでしょう。このとき

　　 ${ 2^1 }$ ー(2倍)→ ${2^2}$ ー(2倍)→ ${2^3}$

と値が2倍ずつ大きくなっていくところに注目すると

　　 ${2^0}$ ー(2倍)→ ${2^1}$

となってくれたらいいのにな、と考えるのが自然です。そこで

　　 ${2^0=1}$

と決めることにしましょう。

同じように考えると

　　 ${2^{-1}}$ ー(2倍)→ ${2^0}$

となって欲しいので

　　 ${ 2^{-1} = \dfrac{1}{2} }$

さらに

　　 ${2^{-3}}$ ー(2倍)→ ${2^{-2}}$ ー(2倍)→ ${2^{-1}}$

となって欲しいので

　　 ${ 2^{-2} = \dfrac{1}{4} = \dfrac{1}{2^2} }$

　　 ${ 2^{-3} = \dfrac{1}{8} = \dfrac{1}{2^3} }$

と決めることにしましょう。

以上まとめると次のようになります。

今回の問題（再掲）

では改めて、今回の問題を掲載しておきます。
自分の力で解いてから、下の解答・解説を読んでみましょう！

f:id:s-uchiyama:20181101233812j:plain

解答

　(1) ${ 4^0 = 1 \cdots }$ (答)

　(2) ${ 3^{-2} = \dfrac{1}{3^2} = \dfrac{1}{9} \cdots }$ (答)

　(3) ${ (-5)^{-3} = \dfrac{1}{(-5)^3} = - \dfrac{1}{125} \cdots }$ (答)

　(4) ${ 0.2^{-2} = \dfrac{1}{0.2^2} = \dfrac{1}{0.04} = \dfrac{100}{4} = 25 \cdots }$ (答)

　(4) (別解) ${ 0.2^{-2} = \left( \dfrac{1}{5} \right)^{-2} = 5^2 = 25 \cdots}$ (答)

解説

(4) (別解)では、次の事実を使っています。結構使えるので、覚えておくことをオススメします。

f:id:s-uchiyama:20181102175925j:plain

今回はここまでです。
最後までお読みいただきありがとうございました！

★もっと演習したい人はコチラ！

★このページが気に入ったら、画面下の「読者になる」をポチッ！

★Facebook・twitter・Instagramのフォローもよろしくお願いします！

★感想・質問は「コメントを書く」からどうぞ！

2018-10-31

指数の拡張１（演習問題）

Stage1 Stage1-14 指数関数・対数関数

f:id:s-uchiyama:20181203003441p:plain

2018-10-30

指数法則（指数関数）

Stage1 Stage1-14 指数関数・対数関数

こんにちは！

数学の部屋のうちやまです。

今回のテーマは「指数法則」です！

指数法則
- 指数法則が成り立つことの確認
例題
- 問題
- 解答
- 解説

指数法則

指数計算を簡単に行うために、次の指数法則があります。

f:id:s-uchiyama:20181104002324j:plain

左側の３つは既に中学数学で学習済みです。今回から、右の２つが新たに加わります。さらに、「指数の拡張１」で指数を整数の範囲まで拡張したので、上の指数法則が ${m}$ と ${n}$ が整数で成り立つことも注目しておきましょう。

指数法則が成り立つことの確認

これらの指数法則が成り立つことを、具体的な例でそれぞれ確認しておきます。

f:id:s-uchiyama:20181104011341j:plain

f:id:s-uchiyama:20181104011348j:plain

f:id:s-uchiyama:20181104011358j:plain

指数法則は形が似ているものがあるので、あやふやな場合はこのように具体的な例で考えてみると良いでしょう。

例題

それでは、指数法則を使って例題を解いてみましょう（自分で解けそうな人はやってみましょう）。

問題

f:id:s-uchiyama:20181104002601j:plain

解答

(1) ${ a^{-3}a = a^{-3+1} = a^{-2} \cdots }$ (答)

(2) ${ a^{-4} \div a^{-2} = a^{-4-(-2)} = a^{-2} \cdots }$ (答)

(3) ${ (a^{-3})^{-1} = a^{-3 \times (-1) } = a^{3} \cdots }$ (答)

(4) ${ (ab^{-1})^3 = a^3 b^{-3} \cdots }$ (答)

解説

(1) の解答を ${a^{-2}}$ としましたが、 ${ \dfrac{1}{a^2} }$ にしなくて良いの？と疑問に思った人もいると思います。数学的にはどちらも同じなので「この形にしないと減点！」ということはありません（もちろん、問題文で特別な指示があれば話は別です）。今回は、問題文でマイナス乗を使っているので、解答も（問題文に合わせて）マイナス乗を使った ${a^{-2}}$ の方を採用しました((3)と(4)も同様です)。

今回はここまでです。

最後までお読みいただきありがとうございました！

2018-10-29

累乗根（指数関数）

Stage1 Stage1-14 指数関数・対数関数

こんにちは！

数学の部屋のうちやまです。

今回のテーマは「累乗根」です！

累乗根とは
累乗根の性質
例題
- 問題
- 解答
- 解説

累乗根とは

累乗根（るいじょうこん）は、中学で学んだ平方根（へいほうこん）を拡張したものです。そこでまず、平方根について簡単に復習しておきましょう。

正方形の一辺の長さ

上図のように、面積が 4 と 3 の正方形の一辺の長さをそれぞれ求めてみることにしましょう。

まず、面積が 4 の正方形の一辺の長さは「2乗して 4 になる数」すなわち「 2 」であることはすぐにわかりますね。

この「2乗して 4 になる数」のことを「 4 の平方根」といいます。この場合、「 4 の平方根（の１つ）は 2 である」という言い方をします。

ちなみに、（の１つ）と書いたのは、2乗して 4 になる数は ${-2}$ もあるからです（ ${ (-2)^2 = 4 }$ ）。よって、正確には「 4 の平方根は ${2}$ と ${-2}$ である」が正しい言い方です。

次に、面積が 3 の正方形の一辺の長さは「2乗して 3 になる数」を考えればよいことがわかります。

この「2乗して 3 になる数」のことを「 3 の平方根」といいます。そして、「2乗して 3 になる数」は、新しい記号を使って ${ \sqrt{3} }$ と表されることは既に中学で学習済みのはずです。

つまりこの場合、「 3 の平方根（の１つ）は ${ \sqrt{3}}$ である」という言い方をします。

この場合も、2乗して 3 になる数は ${ - \sqrt{3} }$ もあるので、正確には「 3 の平方根は ${ \sqrt{3} }$ と ${ - \sqrt{3} }$ である」が正しい言い方です。

累乗根を理解する上では、平方根はこれくらい復習しておけば大丈夫でしょう。では、いよいよ累乗根を紹介します。

立方体の一辺の長さ

f:id:s-uchiyama:20181108152739j:plain

今度は、体積が 8 と 7 の立方体の一辺の長さをそれぞれ求めてみることにしましょう。

先ほどと同じように考えれば、体積が 8 の立方体の一辺の長さは「3乗して 8 になる数」すなわち 2 であることがわかります。

この「3乗して 8 になる数」のことを「 8 の3乗根」といいます。この場合、「 8 の3乗根は 2 」という言い方をします。

さらに、体積が 7 の立方体の一辺の長さは「3乗して 7 になる数」を考えればよいことがわかります。

この「3乗して 7 になる数」のことを「 7 の3乗根」といいます。そして、「3乗して 7 になる数」を、平方根に似た新しい記号を使って ${ \sqrt[3]{7}}$ と表すことにするのです。つまりこの場合「 7 の3乗根は ${ \sqrt[3]{7}}$ 」という言い方をします。

累乗根

同じようにして

「4乗して7になる数」のことを「 7 の4乗根」といい、 ${ \sqrt[4]{7} }$ で表す

「5乗して2になる数」のことを「 2 の5乗根」といい、 ${ \sqrt[5]{2}}$ で表す

一般に

「 ${n}$ 乗して ${a}$ になる数」のことを「 ${a}$ の ${n}$ 乗根」といい、 ${\sqrt[n]{a} }$ で表す

ことにして、これらをまとめて累乗根といいます。

ちなみに、 ${ \sqrt{3} }$ は累乗根の書き方で表せば ${ \sqrt[2]{3}}$ となり、「3の2乗根」ということになりますが、2は省略し、今まで通り「平方根」と呼ぶことにします（3乗根は別名「立方根」と呼ばれます。4乗根以上にはそのような別名はありません）。

累乗根の性質

累乗根には、次の性質が成り立ちます。

f:id:s-uchiyama:20181104131629j:plain

上の３つの公式は、平方根で学んだものとほぼ同じですから理解しやすいと思います。下の２つの公式は初めて出てきましたので、しっかり覚えておきましょう。それぞれの公式の証明については「指数の拡張２」を見てください。

例題

それでは例題を解いてみましょう（自分で解けそうな人はやってみましょう）。

問題

f:id:s-uchiyama:20181104110424j:plain

解答

(1) ${ \sqrt[5]{32} = \sqrt[5]{2^5} = 2 \cdots }$ (答)

(2) ${ \sqrt[4]{2}\sqrt[4]{8} = \sqrt[4]{16} = \sqrt[4]{2^4} = 2 \cdots }$ (答)

(3) ${ \dfrac{ \sqrt[3]{250} }{ \sqrt[3]{2}} = \sqrt[3]{125} = \sqrt[3]{5^3} = 5 \cdots }$ (答)

(4) ${ \displaystyle \sqrt{ \sqrt[3]{729} } = \sqrt[6]{729} = \sqrt[6]{3^6} = 3 \cdots }$ (答)

(5) ${ \sqrt[8]{16} = \sqrt[8]{2^4} = \sqrt{2} \cdots }$ (答)

解説

(1) (2) (3) は問題ないでしょう。(4) (5) は、 ${ \sqrt{a} }$ は ${ \sqrt[2]{a}}$ の2が省略されたものであることを思い出してください。

今回はここまでです。

最後までお読みいただきありがとうございました！

2018-10-28

指数の拡張２（指数関数）

Stage1 Stage1-14 指数関数・対数関数

こんにちは！

数学の部屋のうちやまです。

今回のテーマは「指数の拡張２」です！

指数の拡張
例題
- 問題
- 解答
- 解説

指数の拡張

「指数の拡張１」では、指数を「自然数」から「整数」に拡張しました。今回は、さらに「有理数」まで拡張して、 ${ 2^{\frac{1}{2}}}$ や ${ 2^{\frac{2}{3} }}$ などを考えます。

まず ${2^{\frac{1}{2}}}$ を考えてみます。

「指数の拡張１」では

${2^1}$ ー(2倍)→ ${2^2}$ ー(2倍)→ ${2^3}$

と、隣り合う数の間に成り立つ関係を保たせるために ${2^0}$ や ${2^{-1}}$ などの値を決めました。そこで今回も、隣り合う数の間に成り立つ関係を考え、そこから ${2^{\frac{1}{2} }}$ の値を考えてみましょう。

上の図を見ると

${2^0}$ ー(？倍)→ ${ 2^{ \frac{1}{2}} }$ ー(？倍)→ ${2^1}$

となっています。

よって、「？」に入る数が分かれば、 ${ 2^{ \frac{1}{2}} }$ の値は決まります。

ここで

${2^0}$ ー(２倍)→ ${2^1}$

であることに注目すると、「？」には「2回かけて2となる数」つまり ${\sqrt{2}}$ が入ることが分かります。

よって

${ 2^{ \frac{1}{2}} = \sqrt{2} }$

と決めることにしましょう。

f:id:s-uchiyama:20181104133855j:plain

同じように ${2^{\frac{1}{3}}}$ と ${2^{\frac{2}{3}}}$ を考えてみます。

上の図を見ると ${2^0}$ ー(？倍)→ ${ 2^{ \frac{1}{3}} }$ ー(？倍)→ ${ 2^{ \frac{2}{3}} }$ ー(？倍)→ ${2^1}$ となっています。ここで ${2^0}$ ー(２倍)→ ${2^1}$ であることに注目すると、「？」には「3回かけて2となる数」つまり ${\sqrt[3]{2}}$ が入ることが分かります。よって

${ 2^{ \frac{1}{3}} = \sqrt[3]{2} }$

${ 2^{ \frac{2}{3}} = \sqrt[3]{2} \times \sqrt[3]{2} = \sqrt[3]{2^2} }$

と決めることにしましょう。

以上まとめると次のようになります。

f:id:s-uchiyama:20181104134249j:plain

この基本事項により、「分数乗」と「累乗根」が自由に行き来できるようになります。

さらに指数法則も、指数が有理数の範囲でも使えるようになります。

例題

それでは、この基本事項を使って例題を解いてみましょう（自分で解けそうな人はやってみましょう）。

問題

f:id:s-uchiyama:20181104134539j:plain

解答

(1) $4^{\frac{1}{3}} \times 4^{\frac{1}{4}} \div 4^{\frac{1}{12}} = 4^{ \frac{1}{3} + \frac{1}{4} - \frac{1}{12} }$

${ = 4^{ \frac{6}{12} } = 4^{\frac{1}{2} } = \sqrt{4} = 2 \cdots }$ (答)

(2) ${\displaystyle \left\{ \left( \frac{16}{9} \right)^{-\frac{3}{4}} \right\}^\frac{2}{3} = \left( \frac{16}{9} \right)^{ -\frac{3}{4} \times \frac{2}{3}} }$

$= \left( \frac{16}{9} \right)^{-\frac{1}{2}} = \left( \frac{9}{16} \right)^{\frac{1}{2}}$

${ \displaystyle = \sqrt{ \frac{9}{16} } = \frac{3}{4} \cdots }$ (答)

(3) ${ \sqrt[4]{9} \times \sqrt[6]{27} = 9^{\frac{1}{4}} \times 27^{\frac{1}{6}} }$

${ = (3^2)^{\frac{1}{4} } \times (3^3)^{\frac{1}{6} }}$

${ = 3^{\frac{1}{2}} \times 3^{\frac{1}{2} } = 3 \cdots}$ (答)

(4) ${ \sqrt{a} \div \sqrt[6]{a} \times \sqrt[3]{a^2} = a^{\frac{1}{2}} \div a^{\frac{1}{6}} \times a^{\frac{2}{3}} }$

${ = a^{\frac{1}{2} - \frac{1}{6} + \frac{2}{3} } = a \cdots}$ (答)

解説

(3) (4) から「累乗根は分数乗に直す」と計算が簡単になることがわかります（余力のある人は、(3) (4)を累乗根の性質だけを使って求めてみましょう）。

今回はここまでです。

最後までお読みいただきありがとうございました！

2018-10-27

指数関数のグラフ（指数関数）

Stage1 Stage1-14 指数関数・対数関数

こんにちは！

数学の部屋のうちやまです。

今回のテーマは「指数関数のグラフ」です！

指数関数とは
指数関数のグラフ
- 指数関数のグラフのまとめ
- 底の条件について
指数関数の性質

指数関数とは

${ y = 2^x }$ や ${ y = \left( \dfrac{1}{2} \right)^x }$ のように、 ${ y = a^x }$ の形の関数を指数関数（しすうかんすう）といいます。また、このときの ${a}$ のことを底（てい）といいます。

底には条件があり、 ${ a \gt 0 }$ と ${ a \ne 1 }$ を満たしている必要があります（これについては後ほど詳しく説明します）。

指数関数のグラフ

それでは、指数関数のグラフを考えましょう。例として、 ${ y=2^x }$ と ${ y=\left( \dfrac{1}{2} \right)^x }$ のグラフを考えてみます。

まず、 ${ y = 2^x }$ のグラフは、上図のようにそれぞれの ${x}$ の値に対する ${y}$ の値を求めてみれば、ドンドン増えていくことがわかります。さらにその増え方も、急激に大きくなっていくことがわかります。よって、指数関数 ${ y=2^x}$ のグラフは上図のようになります。グラフを描くときの注意点は次の２点です。

① ${ x=0 }$ のとき ${ y=2^0=1}$ なので、グラフは点 ${ (0,1) }$ を通ります。

② ${x}$ の値が小さくなると ${y}$ の値はドンドン小さくなりますが、0になることはありません。よって、グラフは ${x}$ 軸に触れることはありません（ ${x}$ 軸が漸近線である、という言い方をすることもあります）。

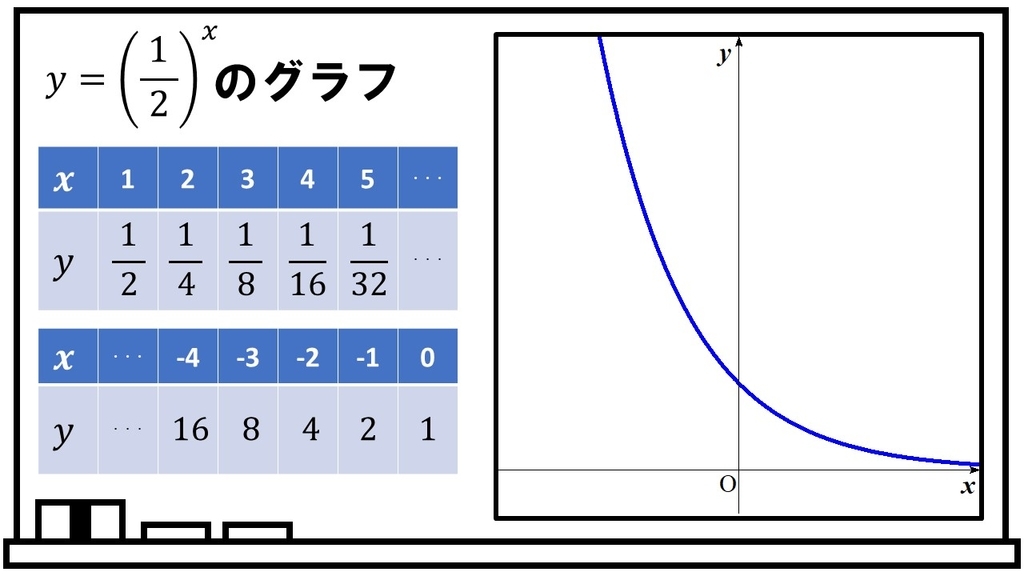
次に、 ${ y = \left( \dfrac{1}{2} \right)^x }$ のグラフも同じように考えていくと、 ${y}$ の値はドンドン(しかも急激に)減っていくことがわかります。よって、指数関数 ${ y=\left( \dfrac{1}{2} \right)^x}$ のグラフは上図のようになります。このときも、グラフを描くときの注意点は次の２点です。

① ${ x=0 }$ のとき ${ y=\left( \dfrac{1}{2} \right)^0=1}$ なので、グラフは点 ${ (0,1) }$ を通ります。 ② ${x}$ の値が大きくなると ${y}$ の値はドンドン小さくなりますが、0になることはありません。よって、グラフは ${x}$ 軸に触れることはありません（ ${x}$ 軸が漸近線である、という言い方をすることもあります）。

指数関数のグラフのまとめ

ここまでの話から、指数関数 ${ y=a^x }$ のグラフは大きく分けて2種類あることがわかります。そしてそれは底の値によって決まり、底が1より大きいとき( ${ a \gt 1 }$ のとき)は、 ${y=2^x}$ のグラフのようにドンドン増加するグラフ、底が1より小さいとき( ${ 0 \lt a \lt 1 }$ のとき)は、 ${ y=\left( \dfrac{1}{2} \right)^x }$ のグラフのようにドンドン減少するグラフになります。まとめるとまとめると下図のようになります。